Humans versus Jack (4)
Computer Bridge 4: Jack Just Isn't Human
(published in Dutch Bridge Magazine IMP February 2006)To gauge the playing strength of Jack, we matched him against seven strong Dutch pairs. This instalment covers the match against internationals Bart Nab and Gert-Jan Paulissen.
Previous instalments reported Jack's success in the first six matches. The seventh and final match was against several-time Dutch champions Nab-Paulissen. Unfortunately, things didn't go as well as against Jack's other opponents. To start with, the laptop crashed and we had to make arrangements to play at a computer at the office of the Dutch Bridge Federation. A bad omen? Well, let's see.
disadvantage
Almost all top players have the same disadvantage when playing against Jack (or any other computer program). They are not used to playing against a computer and they don't know what to expect. However, Gert-Jan Paulissen has a lot of experience with computer bridge. He worked for several years on 'Eindeloos Bridge' (endless bridge) a program known only in the Netherlands. Eindelos Bridge does not play nearly as well as Jack, but Paulissen learned a lot about the way computers 'think' (or rather, are 'taught to think'). So it is no coincidence that Nab and Paulissen, who played with poise and concentration, were able to exploit Jack's weaknesses. They beat Jack by a very large margin, 90-26, earning a well-deserved victory.
We had organised the matches not only to gauge Jack's performance but also to discern where he failed with a view to improving the program. Thus we found it very interesting to analyse the match against Nab-Paulissen. One learns most from one's mistakes.
Of course we knew about Jack's rigidity and credulity, but in the other matches these weaknesses proved nowhere as harmful as against Nab-Paulissen. When computers play against each other, these flaws matter little, but people are clever and flexible enough to take full advantage. Without minimizing the excellent performance of Nab and Paulissen, I would like to focus on Jack's errors. Perhaps such analysis can help us find solutions for the specific problems Jack encounters playing against clever human experts.
For Jack to lose 90 IMPs (while winning only 26) in 28 boards is unusual for Jack. We found six categories to account for this extreme loss.
- Normal actions by Nab and Paulissen that earned them IMPs.
- Excellent bidding and play by Nab-Paulissen.
- Normal actions by Jack that lost IMPs.
- Bad bidding by Jack.
- Bad play by Jack.
- Jack's rigidity and credulity.
Most of the losses occurred in category F. Before looking at some
typical examples, I must explain how Jack 'thinks.' His programmers have
taught him to believe almost everything during the early stages of the
bidding, and to draw firm inferences from the opening lead. Isn't that
normal? If an opponent opens 1  (showing five in
the usual methods) it seems like a waste of time to consider that he might
have (for instance) six clubs and only two hearts. Likewise, if an opponent
opens a 15-to-17 1NT, there is very little reason to take into account the
possibility that he has only 10 HCP. Until shown otherwise, Jack will play
opener for about 15-17 HCP and a fairly balanced hand. Later in the bidding,
and during the play, Jack may have learned more about the deal and will
trust the initial information much less, so his opponents' deviations from
what he expects will not affect him severely. If the play of the cards
indicates that opener just can't have the presumed balanced 15-17 HCP,
Jack will change his initial picture of the hand. However, by then it may
be too late.
(showing five in
the usual methods) it seems like a waste of time to consider that he might
have (for instance) six clubs and only two hearts. Likewise, if an opponent
opens a 15-to-17 1NT, there is very little reason to take into account the
possibility that he has only 10 HCP. Until shown otherwise, Jack will play
opener for about 15-17 HCP and a fairly balanced hand. Later in the bidding,
and during the play, Jack may have learned more about the deal and will
trust the initial information much less, so his opponents' deviations from
what he expects will not affect him severely. If the play of the cards
indicates that opener just can't have the presumed balanced 15-17 HCP,
Jack will change his initial picture of the hand. However, by then it may
be too late.
Playing against other computers that are as reliable as he is, Jack can trust their bidding and opening leads to 'read' the cards accurately without need for mid-course adjustments. Against human opponents things are a bit different...
watch and shiver
In the three deals that follow, Nab and Paulissen told some small 'lies.' Against their human peers, that would have had little effect, but Jack believed everything they told him. Watch and shiver!
Example 1 (directions rotated):
|
| |||||||||||||||||||||||||||||||||||||||
1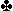 in the 'Dutch Doubleton' system of Nab and
Paulissen may be based on as few as two clubs and is forcing for one round.
Their 1
in the 'Dutch Doubleton' system of Nab and
Paulissen may be based on as few as two clubs and is forcing for one round.
Their 1 response, if not based on diamonds, shows
any 0-7 HCP hand. The rest is natural bidding.
response, if not based on diamonds, shows
any 0-7 HCP hand. The rest is natural bidding.
2 can be beaten, but that is no loss for N/S, as
E/W can make a partscore in clubs. But watch Paulissen make his beatable
contract!
can be beaten, but that is no loss for N/S, as
E/W can make a partscore in clubs. But watch Paulissen make his beatable
contract!
West leads the  10, which rides to South's queen.
Declarer lead the
10, which rides to South's queen.
Declarer lead the  Q to East's king. After taking
two club tricks, the defenders revert to hearts, East playing the
Q to East's king. After taking
two club tricks, the defenders revert to hearts, East playing the
 A and
A and  J to force dummy. So
far, Jack has defended well, as he has succeeded in killing the entry to
dummy's diamonds.
J to force dummy. So
far, Jack has defended well, as he has succeeded in killing the entry to
dummy's diamonds.
However, Paulissen doesn't give up. He leads another diamond to West's ace, producing this ending, with declarer needing the rest of the tricks.
| |||||||||||||||||||
As you can see, West can give East a heart overruff. However, Jack led
the  8. Declarer discarded a heart on dummy's
8. Declarer discarded a heart on dummy's
 J and later ruffed a club in dummy to make his
contract.
J and later ruffed a club in dummy to make his
contract.
Why didn't Jack lead the  9? Very simply, because
South, having 1
9? Very simply, because
South, having 1 , just 'couldn't' have four hearts.
Jack read South for a 4=3=3=3 or 4=3=2=4 pattern, so continuing with the
, just 'couldn't' have four hearts.
Jack read South for a 4=3=3=3 or 4=3=2=4 pattern, so continuing with the
 9 gives a ruff and sluff that might let the
contract make.
9 gives a ruff and sluff that might let the
contract make.
Thus Jack lost 4 IMPs needlessly.
Example 2 (directions rotated):
| |||||||||||||||||||
After East (Nab) opens 1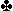 , Jack becomes declarer
in 4
, Jack becomes declarer
in 4 . West can beat 4
. West can beat 4 with
a club lead, but Paulissen leads the
with
a club lead, but Paulissen leads the  6. Lucky Jack?
No way! Nab takes the
6. Lucky Jack?
No way! Nab takes the  A and shifts to the
A and shifts to the
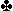 K, which Jack trumps. Next a low heart goes to
dummy's king and East's ace. Jack wins East's
K, which Jack trumps. Next a low heart goes to
dummy's king and East's ace. Jack wins East's  J
return with the
J
return with the  K and draws trump, leaving:
K and draws trump, leaving:
| |||||||||||||||||||
It is easy to see that Jack, who can afford to lose only one more trick,
will make 4 if he plays diamonds from the top.
However, Jack led the
if he plays diamonds from the top.
However, Jack led the  8 and went down one.
8 and went down one.
stupid
Why did he play so stupidly?Actually, it wasn't Jack but Jack's programmers who had erred. WE had specified the Nab-Paulissen opening leads as fourth-best from length and second-best from three small, so Jack assumed rigidly that West's plays of the
 6 followed by the
6 followed by the  2 could
be based on three spades but not four. Trusting this 'card-reading' too
much, Jack played for the diamond finesse that would give him an
overtrick. Alas, instead of an overtrick he wound up with an undertrick, a
swing of 11 IMPs.
2 could
be based on three spades but not four. Trusting this 'card-reading' too
much, Jack played for the diamond finesse that would give him an
overtrick. Alas, instead of an overtrick he wound up with an undertrick, a
swing of 11 IMPs.
If Paulissen deliberately led the  6 to confuse
Jack, it would mean that a rigidly-programmed computer cannot beat flexible
human experts ever. However, it is not necessary to suppose that Paulissen
was trying to deceive Jack. It is common expert practice to lead a high
spot-card from weakness even with length, but Jack had not been programmed
with this knowledge. Give credit where credit is due ... to Paulissen for
choosing the spade spot-card that is most helpful to his partner.
6 to confuse
Jack, it would mean that a rigidly-programmed computer cannot beat flexible
human experts ever. However, it is not necessary to suppose that Paulissen
was trying to deceive Jack. It is common expert practice to lead a high
spot-card from weakness even with length, but Jack had not been programmed
with this knowledge. Give credit where credit is due ... to Paulissen for
choosing the spade spot-card that is most helpful to his partner.
Example 3 (directions rotated):
|
| |||||||||||||||||||||||||||||||||||
West led the  Q. With West having the
Q. With West having the
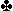 A as an entry, 3NT has no chance. But East ducked
and blocked the hearts---terrible defence!
A as an entry, 3NT has no chance. But East ducked
and blocked the hearts---terrible defence!
Why in heaven's name didn't East unblock his ace? As always, there was
a reason. Jack's programmers had specified a 1NT 'overcall' as showing
about 15-17 HCP. Even allowing for a slight 'underbid,' Jack could not
'bend' enough to picture Paulissen with as much as 20 HCP. So East expected
to beat 3NT several tricks. If he took his  A
immediately he would have to choose between continuing hearts or shifting
to spades. To postpone this decision, he ducked the first heart, allowing
declarer to play on clubs for nine tricks and a 17-IMP swing.
A
immediately he would have to choose between continuing hearts or shifting
to spades. To postpone this decision, he ducked the first heart, allowing
declarer to play on clubs for nine tricks and a 17-IMP swing.
This error is hard for us simple human beings to understand, but it is
nothing special for a computer without nerves. Jack could have succeeded,
however, had his programmers described South's 1NT as showing 15-20 HCP.
Then, uncertain of beating 3NT by ducking the  A,
East would have taken the first heart and continued the suit to ensure the
defeat of the contract.
A,
East would have taken the first heart and continued the suit to ensure the
defeat of the contract.
Actually, credit must again be given to Paulissen, who knew what few human bridge players know: that a 1NT 'sandwich' (a bid coming between two opposing bidders) shows a hand about as good as the one he had, a full trick stronger than a strong 1NT opening. Paulissen was simply making the right bid, not trying to deceive poor Jack. So, should Jack be programmed to expect 18-20 HCP for a 1NT sandwich?
Not really, even though this is an appropriate range. For most human opponents still bid 1NT sandwiches with 15-17 HCP. To read this sequence correctly, Jack must know not only good bidding, but also how much his opponents know!
It is obvious that Jack must learn to be much more flexible. That sounds very logical, but it masks the real problem. Bridge is a game in which full disclosure plays an important role. Players must explain their partnership agreements upon request, but they need not explain what they know from bridge logic. In Example 3, a human East might suspect that South had more than 17 HCP, and thus might inquire, but Jack has no 'sixth sense,' let alone the ability to ask a direct question. He depends entirely on the information about his opponents' methods that has been given by his program.
full disclosure
Why did we make Jack so rigid? Wasn't it better to make a more flexible
program? The answers to these questions are very simple. The early bidding
and the opening lead are very reliable. It would be a waste not to trust
this information to narrow Jack's construction of the unseen hands as much
as possible. In fact, it is costly not to do so. When computers play
against each other, the programmers are very strict about full disclosure.
As soon as a call deviates from normal expectation, opponents are given
this information to enter in their program. In Example 1 this might be:
'The 1 rebid does not deny four hearts.' Using this
procedure, in all three examples we could have informed Jack of
possibilities that he would not otherwise expect.
rebid does not deny four hearts.' Using this
procedure, in all three examples we could have informed Jack of
possibilities that he would not otherwise expect.
At the table, however, things are not that simple. Would a human being have asked, and would the answer have helped him? If so, then Jack should have gotten all the extra information. But do you have to be a good player to think of these questions? And is Jack such a good player?
To avoid raising the issue of whether Jack's team was helping him illicitly during the matches, we had decided beforehand to leave Jack on his own without asking questions at the table. It is clear that this handicapped Jack when playing against Nab-Paulissen. Had we taken notice of the problems shown by the three examples, and made the appropriate corrections, Jack would have lost by about 32 IMPs instead of 64---still a big win for Nab-Paulissen, but more in keeping with the real difference in strength.
So using imagination and judgement in ways that will not confuse your partner gives you a big advantage against Jack. That is, if you don't tell Jack what might be going on and his programmers have not anticipated it.
Importantly, we have learned from these matches that disclosure about partnership methods when playing against human opponents is different from disclosure when playing against other computers. If Jack is to play matches against humans again, some clear procedures for more thorough disclosure must be provided.
By the way, letting Jack ask is not a good remedy. If permitted, Jack might ask hundreds of questions (most of them trivial) on every deal. A few years ago Matt Ginsberg, GIB's programmer, suggested this solution, interpreting 'full disclosure' as the right to ask countless questions. That sounds reasonable, but if implemented it could lead to questions of the form, 'What would your program bid with this hand?' repeated for each of the myriad hands that might be encompassed by any given call. Such an inventory, of course, is not intended by the requirement for 'full disclosure.' Bridge is still a game in which inference and judgment must always play an important role.
The matches have given us very useful material, and we thank the pairs that joined our experiment. We hope they will cooperate again in the future!
The final results:
| Jack | - | Bart Nab & Gert-Jan Paulissen | 26 - 90 | |
| Jack | - | Paul Felten & Eric van Valen | 43 - 60 | |
| Jack | - | Erik Janssen & Jeroen Top | 43 - 51 | |
| Jack | - | Vincent Ramondt & Berry Westra | 45 - 53 | |
| Jack | - | Jan van Cleeff & Vincent Kroes | 61 - 46 | |
| Jack | - | Hanneke Kreijns & Just vd Kam | 74 - 53 | |
| Jack | - | Ton Bakkeren & Huub Bertens | 67 - 32 | |
Wim Heemskerk